|
|
| Artikler |
|
Robot Netværk Tele Installationer Lys Komponenter Elektronik Cases Håndværk Elektroteknik Historien Af interesse |
| Diverse |
|
Opslag Billedopslag FAQ Video Links Om |
 Tilpasset søgning |
Effektivværdi
| Dokument oprettet: | 7 Jan 2009 |
| Senest ændret: | 24 Apr 2021 |
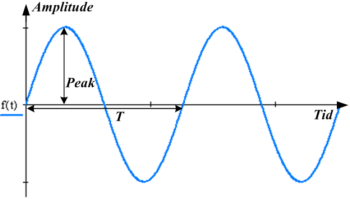 Effektivværdien for en tidsvarierende strøm i eller spænding u er som oftest den størrelse, der har interesse ved angivelsen af en given strøm eller spænding (andre karakteristiske størrelser er fx middelværdi og peak-værdi). Stikkontakters pålydende spænding på 230 V er fx udtrykt ved effektivværdien. Rent tidsmæssigt veksler stikkontaktens spænding sinusformet med en øvre og nedre peak-værdi på henholdsvis 325 V og -325 V.
Effektivværdien for en tidsvarierende strøm i eller spænding u er som oftest den størrelse, der har interesse ved angivelsen af en given strøm eller spænding (andre karakteristiske størrelser er fx middelværdi og peak-værdi). Stikkontakters pålydende spænding på 230 V er fx udtrykt ved effektivværdien. Rent tidsmæssigt veksler stikkontaktens spænding sinusformet med en øvre og nedre peak-værdi på henholdsvis 325 V og -325 V.
En periodisk varierende strøm eller spænding udtrykt ved effektivværdien betyder, at der vil afsættes præcis den samme effekt i en tilsluttet modstand som en jævnstrøm eller jævnspænding med samme pålydende værdi vil afsætte. Det er denne egenskab, der karakteriserer effektivværdien. Det følger, at effektivværdien for fx en given jævnspænding er enslydende med jævnspændingen selv.
Effektivværdien benævnes også RMS-værdien - RMS for Root Mean Square. Denne betegnelse skyldes, at effektivværdien Feff af en given størrelse beregnes som kvadratroden af middelværdien af den aktuelle størrelse kvadreret (f 2(t)). Matematisk ser det for en periodisk funktion, et kurveforløb, der gentager sig selv med periodetiden T, således ud:
Det lange s-formede symbol er et integraletegn. Med integralregning kan arealet under en kurve bestemmes. Ved at tage integralet (bestemme arealet under kurven) fra tiden 0 til periodetiden T (angivet som grænser på integraletegnet) og derefter dele med T opnås en middelværdi af det kvadrerede funktionsudtryk f 2(t).
Eksempel på udregning af en effektivværdi
Hvad er effektivværdien for en savtakket kurveform?Effektivværdien kan udregnes symbolsk med henblik på en generel formel for alle kurver af samme type. Savtakken har periodetiden T og peak-værdien P. Funktionsforskriften for savtakken (for en enkelt periode) er følgende.
Funktionsforskriften for kurven sættes ind i formlen for RMS-værdien.
Regneudtrykket kan løses ved håndkraft eller det kan løses med en regnemaskine. Her løses det med TI-89.
Resultatet i regnemaskinen (den numeriske peak-værdi P multipliceret med √3 delt med 3) kan også skrives som peak-værdien delt med √3 eftersom √3/3 er lig med 1/√3.
Effektivværdier for karakteristiske kurveformer
For en række karakteristiske kurveformer kan følgende tabel opstilles mht effektivværdier.
| Kurve |
Effektivværdi |
|
|---|---|---|
| Sinus |  |
 |
| Sinus gennem fuldbro |  |
 |
| Sinus gennem halvbro |  |
|
| Trekant | 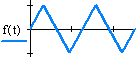 |
 |
| Savtak |  |
 |
| Firkant |  |
|
Ved hjælp af grundformlen for effektivværdien kan der, som i ovenstående tabel, udarbejdes simplere formler (uden integraler) for effektivværdien af en given kurveform. En kurve som nedenstående, eller kombinationer af den, kan man støde på inden for effektelektronik.
Effektivværdien for ovenstående kurveform er som følger.
Interne links til emner i dette opslag:
- Den effektive strømstyrke, I (Hvad er harmoniske strømme?)
- Grænselastintegrale
- Root mean square [wikipedia.org]
| Home | | | Copyright © 2002-2026 Cubus | cubusadsldk@gmail.com |

